Deciphering common principles
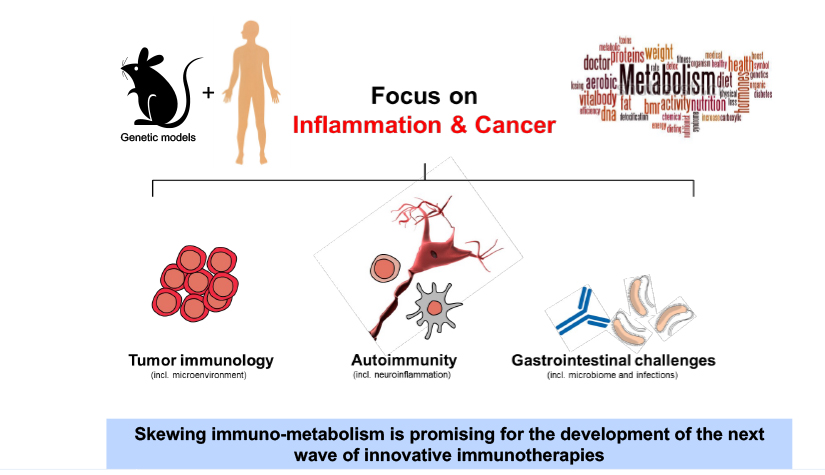
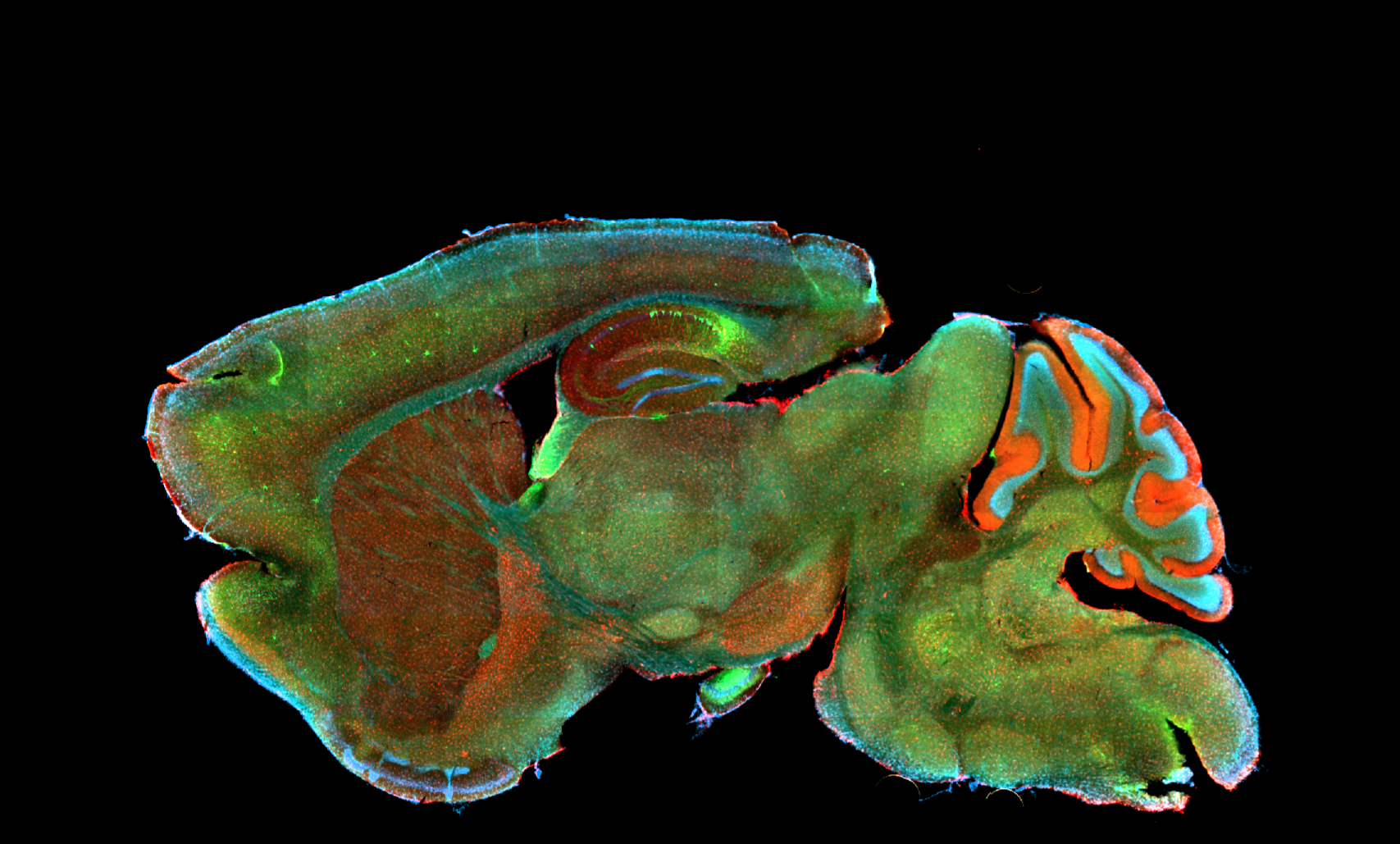
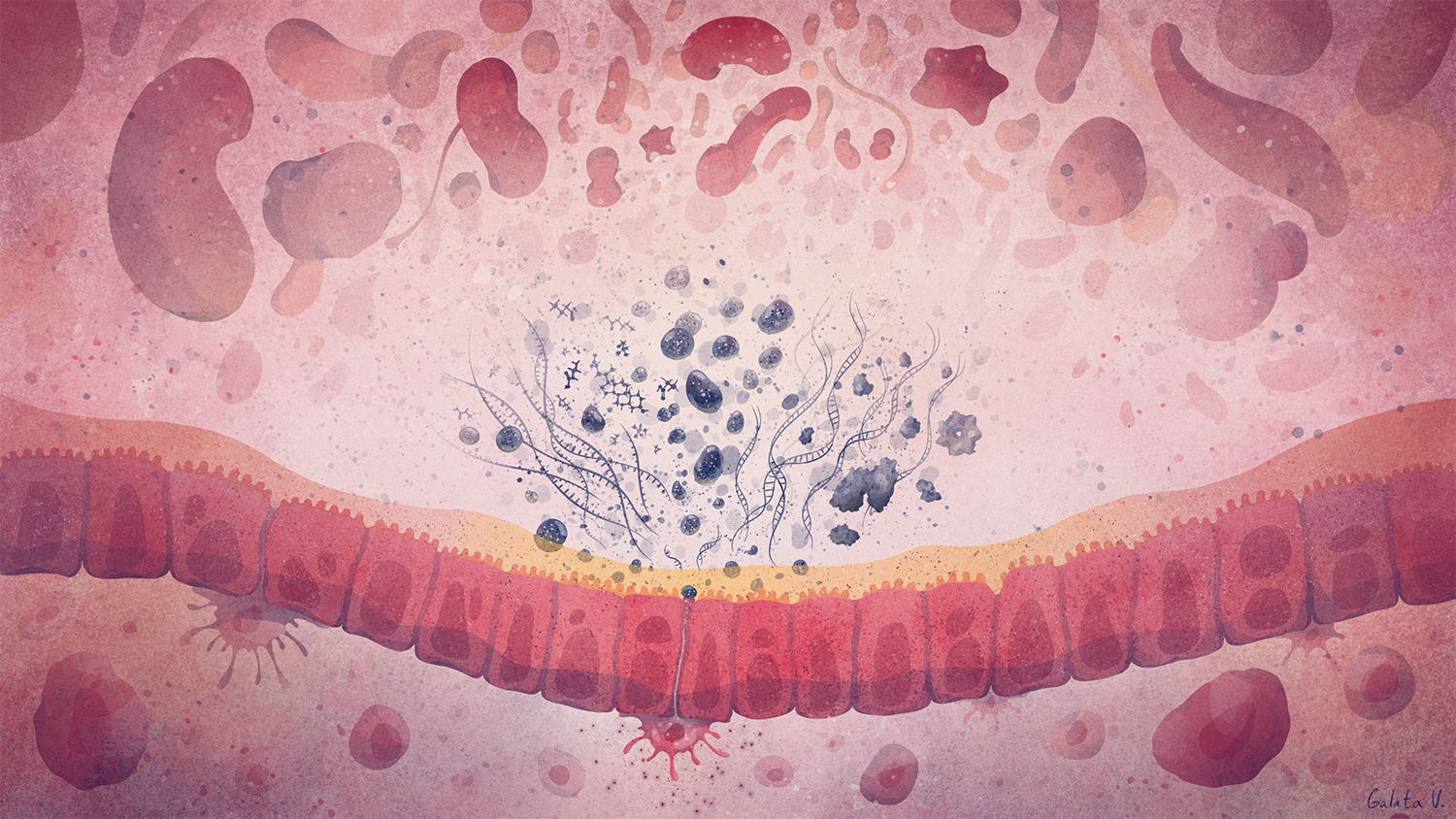
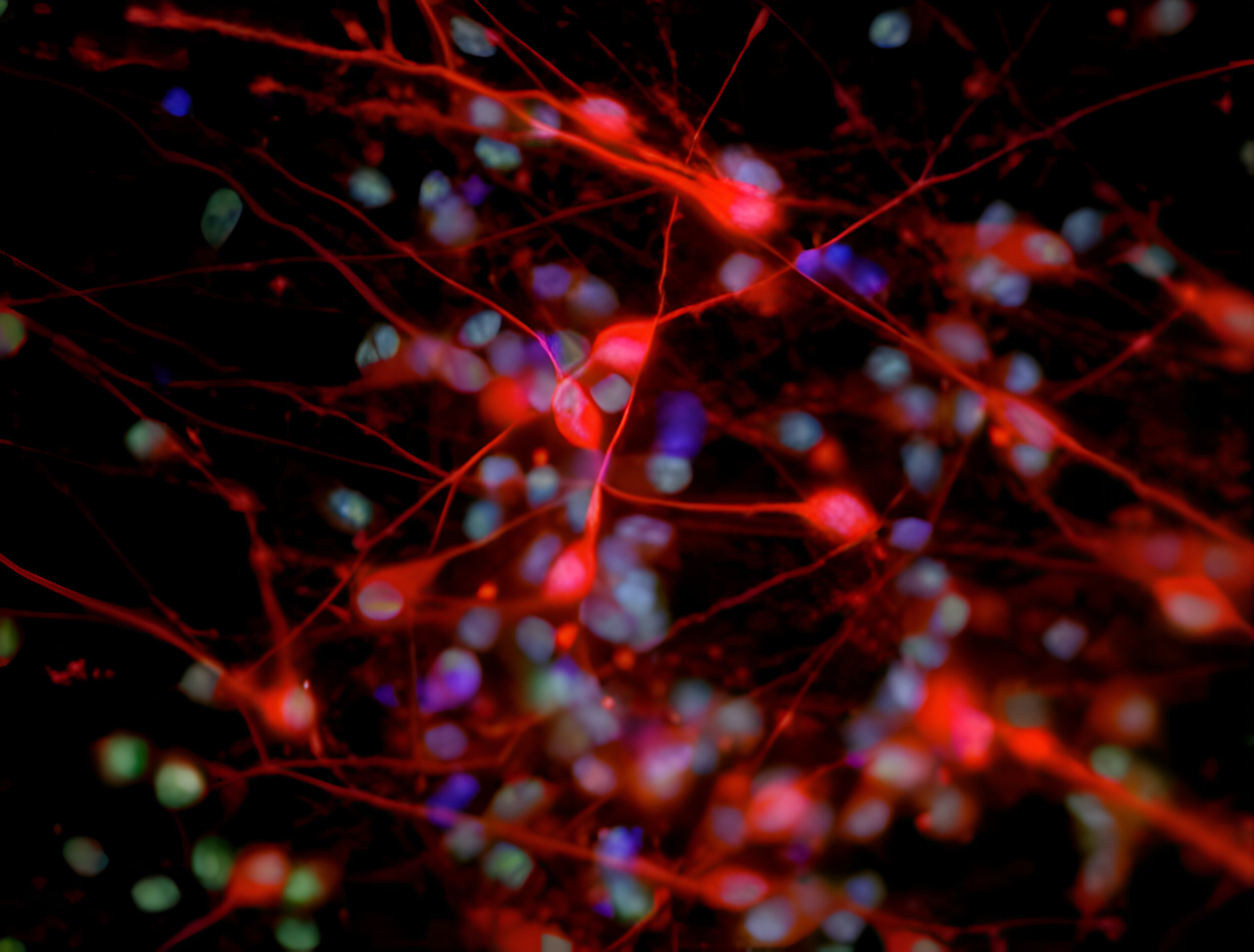
We aim to understand underlying mechanisms and the interplay of disease-influencing factors to better diagnose, treat and prevent neurodegeneration. Hence, we approach those diseases from many angles. Be it interactions with microbial communities, metabolic networks, neuroinflammation or cell fate determination, the systems we study are diverse. Yet, they share similarities and guiding principles.